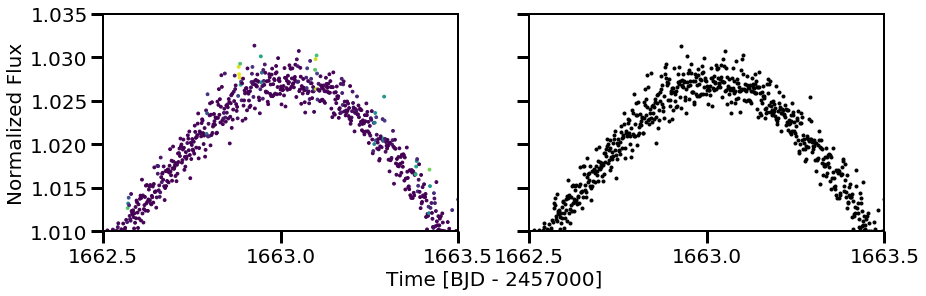Other Fun Features

Some other features that are included in the \(\texttt{stella}\) package include finding rotation periods and fitting flares with a simple analytic model to extract parameters such as the equivalent duration. Here, we will go through each of these additional modules.

import os, sys
sys.path.insert(1, '/Users/arcticfox/Documents/GitHub/stella/')
import stella
import numpy as np
from tqdm import tqdm_notebook
import matplotlib.pyplot as plt

plt.rcParams['font.size'] = 20

First thing’s first: we need a light curve! We’re going to use the same one that has been used in the previous demonstrations.

from lightkurve.search import search_lightcurvefile
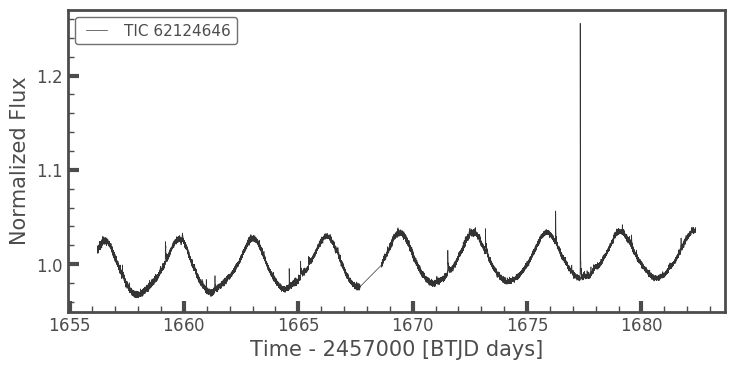
lc = search_lightcurvefile(target='tic62124646', mission='TESS')
lc = lc.download().PDCSAP_FLUX.normalize()
lc.plot()
lc = lc.remove_nans()

//anaconda3/lib/python3.7/site-packages/lightkurve/lightcurvefile.py:47: LightkurveWarning: `LightCurveFile.header` is deprecated, please use `LightCurveFile.get_header()` instead.
  LightkurveWarning)

1.1 Measuring Rotation Periods

To measure the rotation period of a light curve, you need the following information: a target ID (can be anything you want), a time array, a flux array, and a flux error array. These can all be retrieved from the \(\texttt{lightkurve}\) object. Then, you initialize the class \(\texttt{stella.MeasureProt}\).

mProt = stella.MeasureProt([lc.targetid], [lc.time], [lc.flux], [lc.flux_err])

The rotation measurement tool used in this class is a Lomb-Scargle Periodogram. You have the option the set the minimum frequency (minf=1/12.5) and maximum frequency (maxf=1/0.1) that the periodogram searches over. You can also set the samples per peak (spp=50). The default values are noted in parentheses.

mProt.run_LS()

Finding most likely periods: 100%|██████████| 1/1 [00:00<00:00, 29.80it/s]

Calling this will create an \(\texttt{astropy.table.Table}\) attribute with some metrics about the rotation period measured in that light curve. The columns in this table include: - Target_ID: the ID for that light curve. - period_days: the period as measured in the first orbit. - secondary_period_days: the period as measured in the second orbit. - gauss_width: the width of a best-fit Gaussian to the most likely period. - max_power: the power of the periodogram at the most likely period. - orbit_flag: a combined flag per orbit (0 = reliable measurement). - oflag1: period flag for the first orbit (0 = reliable measurement). - oflag2: period flag for the first orbit (0 = reliable measurement). - Flags: Defines a flag based on all observations of the given target. This mainly applies to stars observed in multiple sectors, otherwise it is the same value as the orbit_flag (0 = reliable measurement). - avg_period_days: the average most likely period for that target. This is averaged over multiple sectors when available.

Note that by fitting to each orbit, we are limiting the period search space to relatively short rotation periods.

mProt.LS_results

Table length=1

Target_ID	period_days	secondary_period_days	gauss_width	max_power	secondary_max_power	orbit_flag	oflag1	oflag2	Flags	avg_period_days
int64	float64	float64	float64	float64	float64	float64	float64	float64	int64	float64
62124646	3.2296791476459177	3.2163622471188593	0.3318830648048035	0.94813902363263	0.1934361751924491	0.0	0.0	0.0	0	3.2296791476459177

For this star, we find a period of 3.23 days. We can fold over this period in \(\texttt{lightkurve}\) to see if this period is found in the light curve:

lc.fold(mProt.LS_results['avg_period_days'].data[0]).plot()

<matplotlib.axes._subplots.AxesSubplot at 0x14ca0c400>

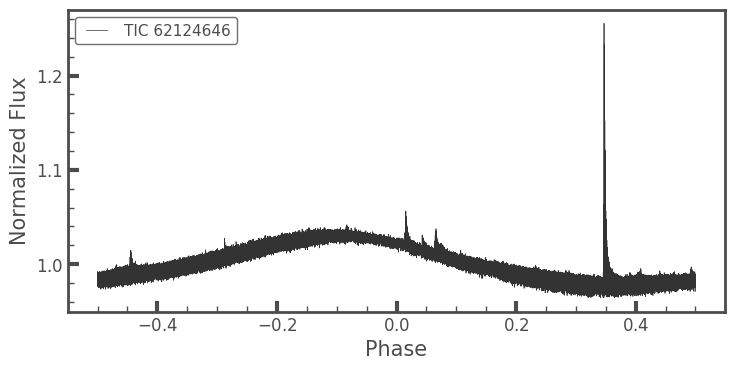
That looks nice! (And so do those flares!!)

1.2 Fitting Flares

In \(\texttt{stella}\), we use a very basic model flare fit of a sharp rise and an exponential decay. This can be done through a class included in the code. The first thing that needs to be done is get predictions for where the flares occur.

MODEL_DIR = '/Users/arcticfox/Documents/flares/run01/'
MODEL = [os.path.join(MODEL_DIR,i) for i in
          os.listdir(MODEL_DIR) if i.endswith('.h5')][0]

cnn = stella.ConvNN(output_dir='.')
cnn.predict(modelname=MODEL,
            times=lc.time,
            fluxes=lc.flux,
            errs=lc.flux_err)

WARNING: No stella.DataSet object passed in.
Can only use stella.ConvNN.predict().

100%|██████████| 1/1 [00:00<00:00,  1.16it/s]

Again, now we have a light curve with predictions from just one of the \(\texttt{stella}\) models.

plt.figure(figsize=(14,4))
plt.scatter(cnn.predict_time[0], cnn.predict_flux[0], c=cnn.predictions[0], vmin=0, vmax=1)
plt.xlabel('Time [BJD - 2457000]')
plt.ylabel('Normalized Flux');

Now we can initiate our flare fitting class, stella.FitFlares, and start fitting those flares!

ff = stella.FitFlares(id=[lc.targetid],
                      time=[lc.time],
                      flux=[lc.flux],
                      flux_err=[lc.flux_err],
                      predictions=[cnn.predictions[0]])

The flares are identified given a certain probability threshold (here, I use a threshold of 0.5, which is what was used in Feinstein et al. (2020)). For the cleanest sample of flares, one could explore a higher probability threshold.

Several parameters about the flare are returned in an astropy Table: - tpeak: the peak time of the flare - amp: the amplitude of the flare - dur_min: the duration of the flare, given in minutes - rise: how quickly the flare goes off (this is very fast and generally the same across all flares) - fall: the exponential decay - prob: the probability at the tpeak time

ff.identify_flare_peaks(threshold=0.5)

ff.flare_table

Finding & Fitting Flares: 100%|██████████| 1/1 [00:00<00:00,  3.06it/s]

Table length=16

Target_ID	tpeak	amp	dur_min	rise	fall	prob
float64	float64	float64	float64	float64	float64	float64
62124646.0	1656.4576694743778	0.005172718665542601	39.030702680360896	0.0001	0.0068845897686542765	0.9807868599891663
62124646.0	1657.3132433819856	0.009350702285110113	46.042747492602345	0.0001	0.00544053135707717	0.9993744492530823
62124646.0	1659.1882815389308	0.01651105340402831	39.06894305336602	0.0001	0.004866570925370507	0.9999998807907104
62124646.0	1659.9327402342174	0.005312998537809568	39.043420341455345	0.0001	0.009961509221298924	0.6145604252815247
62124646.0	1661.3591548909953	0.016160458326441446	40.0714874834236	0.0001	0.005478654540630172	0.9998658895492554
62124646.0	1664.6022613763535	0.01929075100398181	40.123127932126195	0.0001	0.008377466696227073	1.0
62124646.0	1665.1050461281989	0.013147137094216875	39.089653189007684	0.0001	0.008085791885095953	0.9999781847000122
62124646.0	1671.5384179782993	0.020358612261051418	39.123105861217994	0.0001	0.007760436890183154	1.0
62124646.0	1673.1870273690974	0.02055904063986008	39.11462778501233	0.0001	0.00705477984045044	1.0
62124646.0	1676.253683697338	0.030555546845416823	39.21423214992252	0.0001	0.009013828081917988	1.0
62124646.0	1676.9550688450404	0.006738771249223156	39.02549994422418	0.0001	0.004630533925748051	0.997788667678833
62124646.0	1677.3245111133422	0.28101439352385976	40.42962776711578	0.0001	0.006564764007629262	1.0
62124646.0	1677.7953414701415	0.008595585280516745	39.0421747490553	0.0001	0.0062489050043089325	0.9562909603118896
62124646.0	1679.1647760003075	0.0061154840825841305	39.03564755886011	0.0001	0.0071376024321586715	0.9747272729873657
62124646.0	1679.571717154592	0.009053494981558293	39.0635014475265	0.0001	0.008884838879720103	0.9999923706054688
62124646.0	1681.7341971978394	0.010642664416901192	39.032176560598906	0.0001	0.003402254154151447	0.9999966621398926

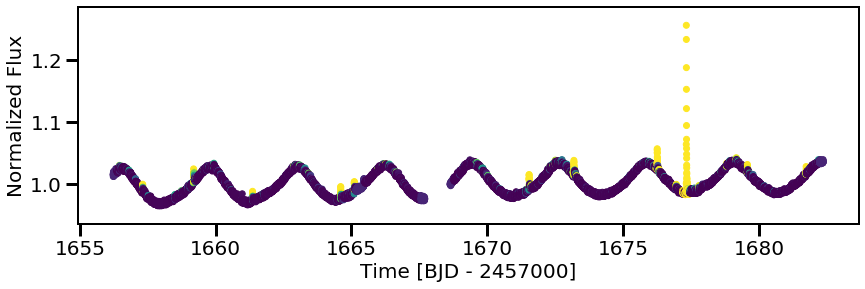
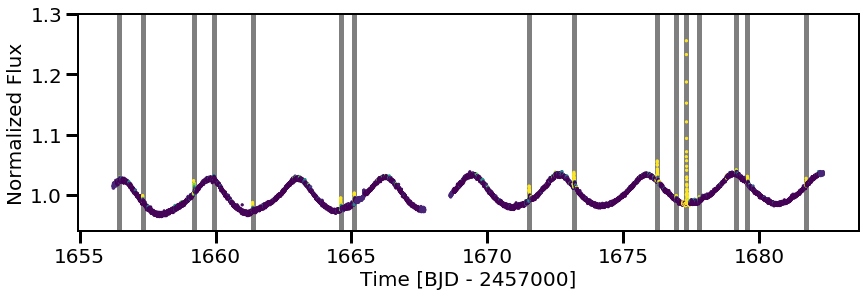
Cool! We can mark all of our flares as well, just to see them better by-eye:

plt.figure(figsize=(14,4))
plt.scatter(ff.time[0], ff.flux[0], c=cnn.predictions[0], s=5)

for tpeak in ff.flare_table['tpeak']:
    plt.vlines(tpeak, 0,2, color='k', alpha=0.5, linewidth=5, zorder=0)

plt.ylim(0.94,1.3)
plt.xlabel('Time [BJD - 2457000]')
plt.ylabel('Normalized Flux');

plt.figure(figsize=(14,4))
plt.scatter(ff.time[0], ff.flux[0], c=cnn.predictions[0], s=5)
for tpeak in ff.flare_table['tpeak']:
    plt.vlines(tpeak, 0,2, color='k', alpha=0.5, linewidth=5, zorder=0)
plt.xlim(1660,1666)
plt.ylim(0.96,1.05)

(0.96, 1.05)

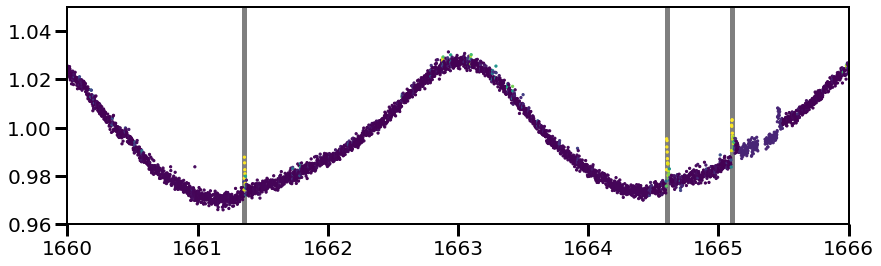
You’ll also note there is a flare at time$:nbsphinx-math:`sim`$1665.5 that was not identified. As there was a significant gap in the data and the CNN cannot handle data gap, the cadences around this region were ignored. Hence, that flare was not identified.

Additionally, the light curve looks to have a few flares at time$:nbsphinx-math:`sim`$1663. Zooming in, these don’t look like flares. This is better seen when the eye is not guided by the prediction assignment of the neural network:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(14,4), sharex=True, sharey=True)
ax1.scatter(ff.time[0], ff.flux[0], c=cnn.predictions[0], s=8)
ax2.plot(ff.time[0], ff.flux[0], 'k.')
for tpeak in ff.flare_table['tpeak']:
    plt.vlines(tpeak, 0,2, color='k', alpha=0.5, linewidth=5, zorder=0)
plt.xlim(1662.5,1663.5)
plt.ylim(1.01,1.035)
plt.xticks(np.arange(1662.5, 1664.0, 0.5))
ax1.set_ylabel('Normalized Flux')
ax1.set_xlabel('Time [BJD - 2457000]', x=1.1)

Text(1.1, 0, 'Time [BJD - 2457000]')